Static Equilibrium
Static equilibrium is the condition that obtains when all the forces acting on an object are in balance.
1 Forces, Moments, Torques, and Couples
Definition 1 (Force) A force is a vector which can accelerate a certain mass by a known acceleration. When multiple forces are combined on a single point, they act together by the sum of their vectors.
Definition 2 (Moment) A moment is the result of a force offset from a point by a certain distance, which has a tendency to cause rotational motion about that point. To find the resulting acceleration about a point caused by a particular moment vector, take the cross product of that moment vector with the vector from the point to the base of the moment.
Since a moment is F \, a where a is the length of the lever arm to the force, the units of a moment are m l^2 t^{-2}.
When you have a force that is offset from the perpendicular axis to a point, you can either separate the force into horizontal and vertical components, or you can take the perpendicular line from the point to the extension of the force vector.
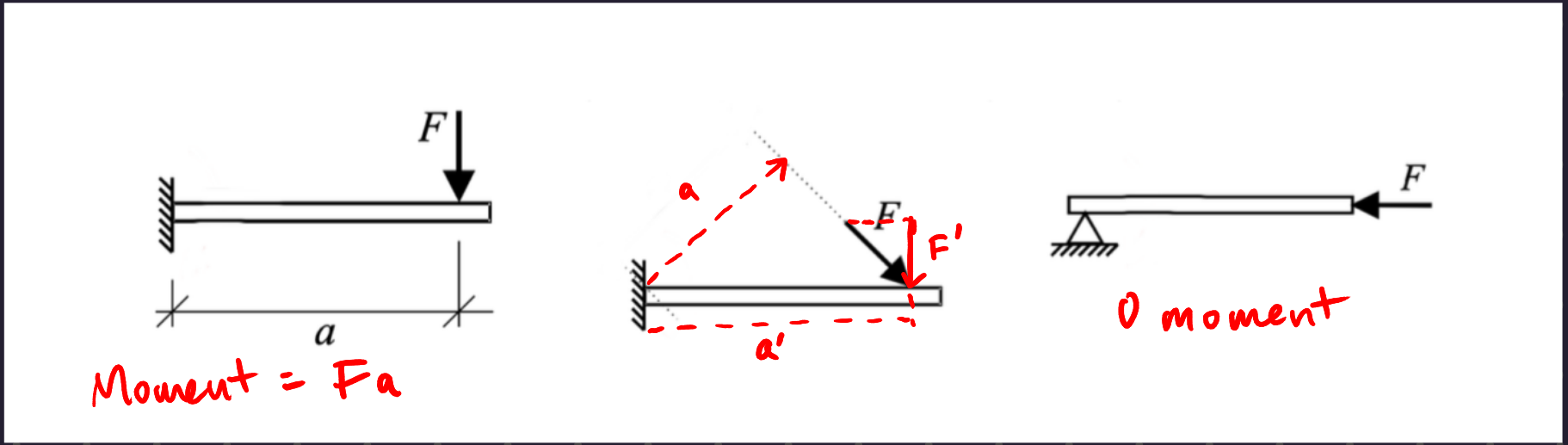
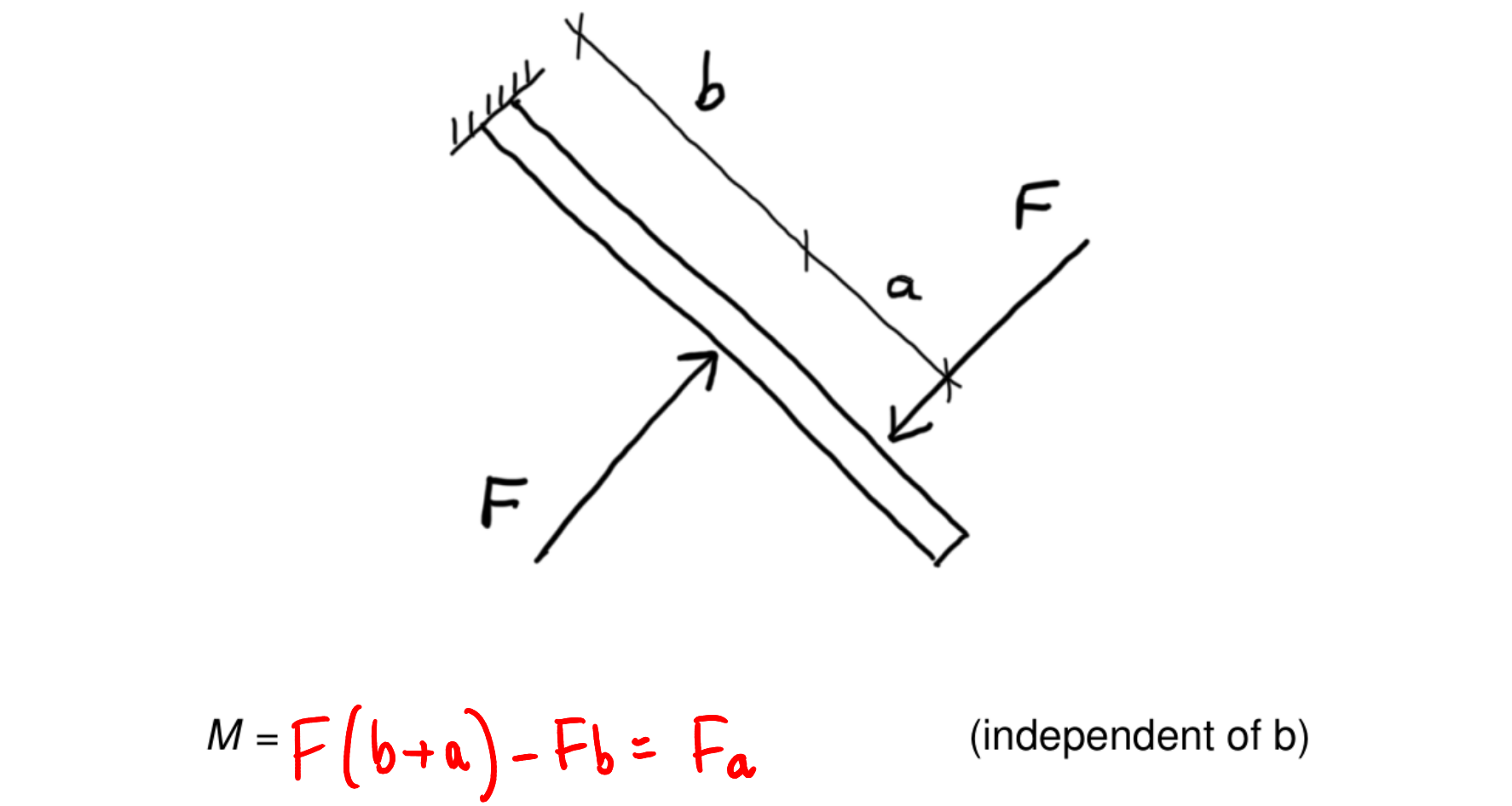
Definition 3 (Couple) A couple is a moment created by two equal and opposite forces with a distance between them. The moment produced by a couple about a point is independent of the distance of that point from the couple.
You can indicate a couple with the following drawing:
Definition 4 (Torque) A torque is a moment applied about the axis of a structural member, created as the result of a couple. They are distinct from bending moments, which act perpendicular to the axis of a structure.
Bending moments keep planar elements within the plane, but torque moments act outside of the plane.
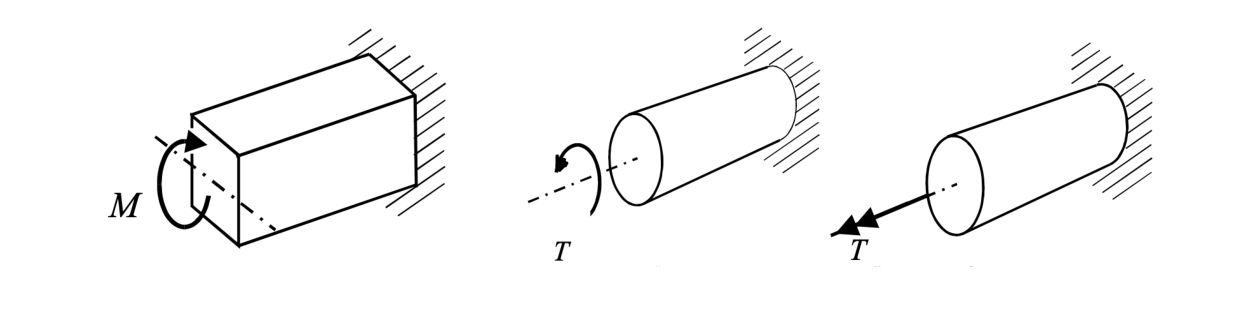
The best way to draw torque is with the double-headed vector, and the resulting torque is determined by the right hand rule. Methods 2 and 3 show toque in the same direction.
2 Applied loads
Many actions can apply loads to a structure, some of which are more certain than others.
2.1 Live loads
Loads that change as the structure is used. In a room, the people are a live load, as are the furniture.
2.2 Dead loads
Dead loads are created by the weight of the structure itself. These don’t really change over the life of the structure.
The expected loading of a structure informs the safety factor when creating a design.
2.3 Reaction forces
These are created by a support. Note that supports are usually assumed to take both upwards and downwards loads!
3 Static Equilibrium
If a structure is sitting and not moving (as one would generally prefer a structure to be), it is in static equilibrium. If a structure is not accelerating, then the net force on that structure is zero.
Structures in this class will be analyzed in the y-z plane.
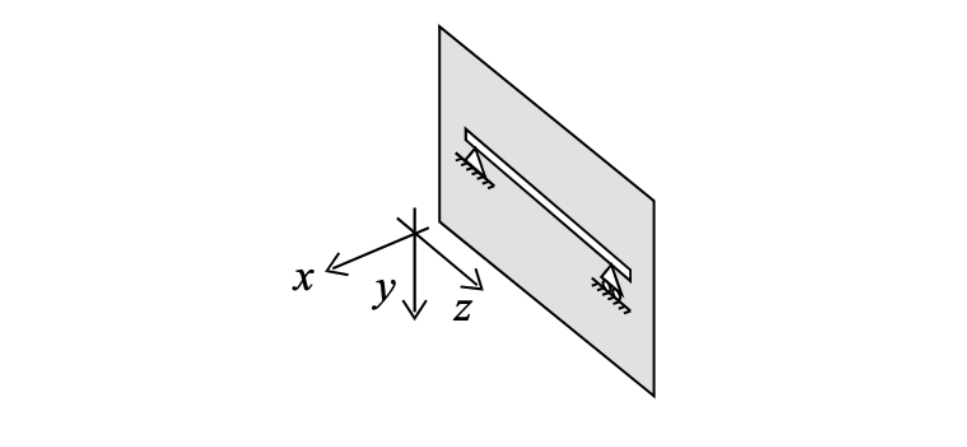
Since we’re analyzing planar structures, three fundamental equations apply:
- Horizontal equilibrium \Sigma F_z = 0 \tag{1}
- Vertical equilibrium \Sigma F_y = 0 \tag{2}
- Moment equilibrium \Sigma \, M_x = 0 \tag{3}
3.1 Support requirements.
Every structure in 2D space needs at least 3 reaction forces to achieve static equilibrium. With less than 3 forces, it cannot achieve static equilibrium; and with more than 3 forces the structure will often be statically indeterminate, i.e. rather than a particular solution there will exist a family of solutions which satisfy the boundary conditions.
This leads us to the classic support for a bridge, where one side is supported by a pin only and the other side is supported by a pin and roller.
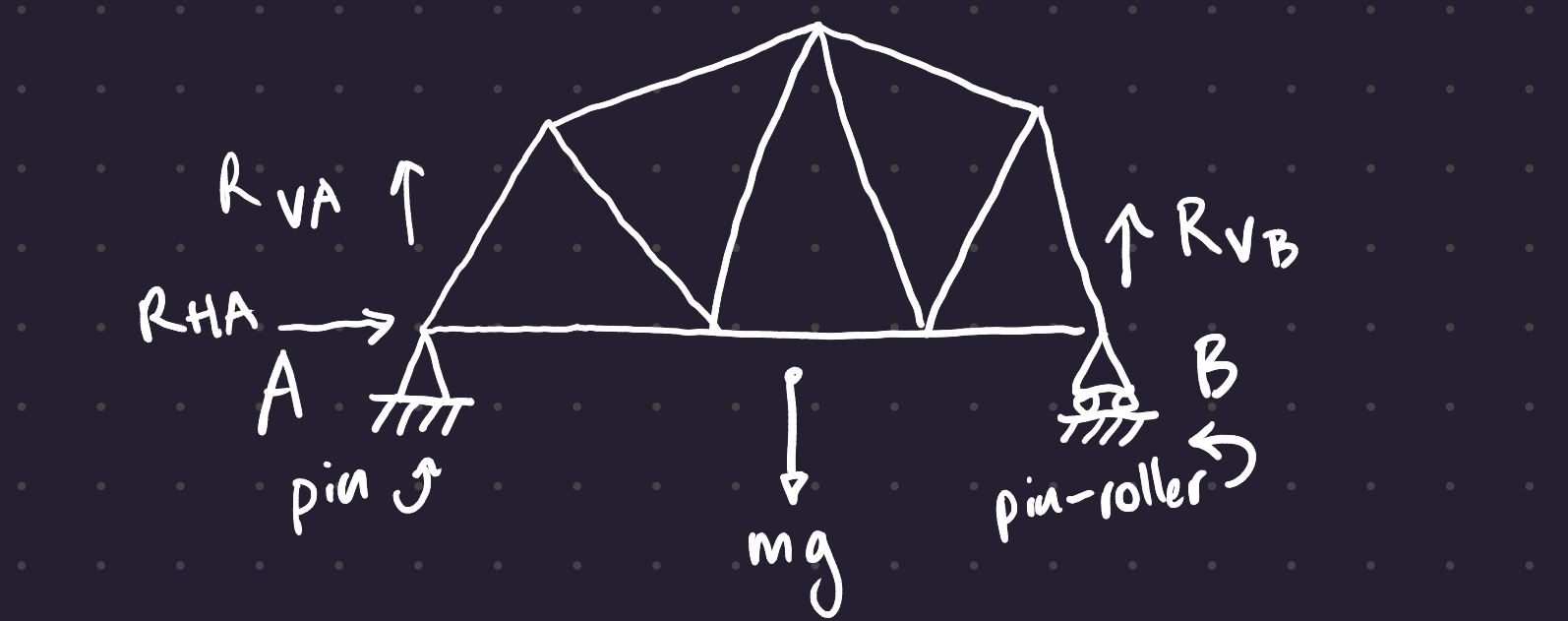
Note that in the example above, since we know from Equation 1 that \Sigma F_z = 0, the reaction force R_{AH} must equal zero (there are no other forces to balance it). Had we used two pinned supports instead, we would not be able to determine the horizontal components of the reaction forces.
A fixed support has all 3 reaction forces F_y, F_z, and M.
Your first job in a structural mechanics question is to find the support reactions created by the supports.
4 Static Determinacy
Maxwell’s rule looks at the number of internal bars and pins within a structure to determine whether the structure is internally statically determinate. This is beyond the scope of this course.
Here we examine external determinacy only. We examine whether the support reactions can be determined through equilibrium alone (equilibrium calculations result in a single value for the support reactions). With a statically determinate structure, any damage at any point is immediately enough to make the structure fail catastrophically; with a redundant (indeterminate) structure this is not the case.
Basically, for a structure to be externally statically determinate, it must have the minimum number of reaction forces and members necessary to support it.