1 Structural Mechanics 2
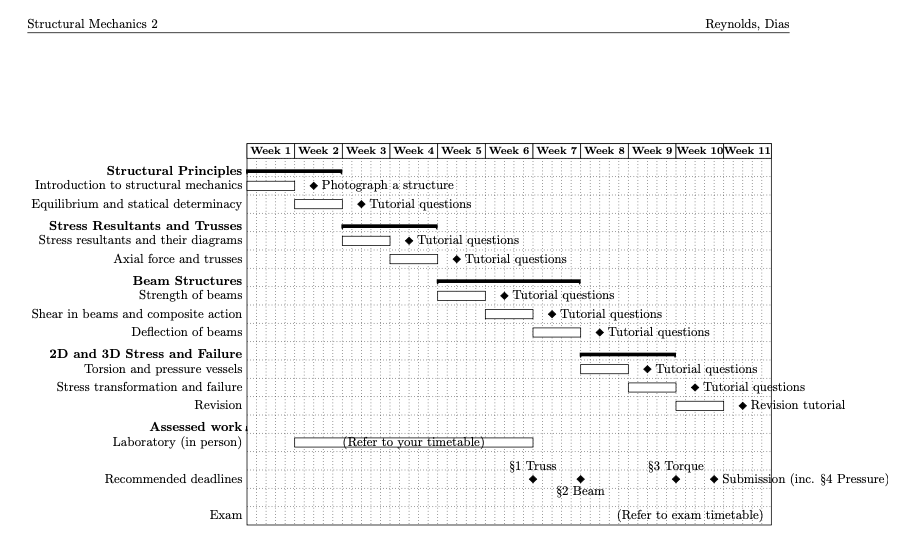
1.1 Course Outline
| School | School of Engineering | College | College of Science and Engineering |
|---|---|---|---|
| Credit level (Normal year taken) | SCQF Level 8 (Year 2 Undergraduate) | Availability | Available to all students |
| SCQF Credits | 10 | ECTS Credits | 5 |
1.2 Summary
This course engages students with the fundamental principles of Structural Mechanics relevant to civil and mechanical engineers. Specific topics including: equilibrium, stress, strain, axial load, torsion, bending, shear, and deflections in structural elements including beams, columns, struts, ties, and trusses.
1.3 Course Description
T1 Introduction and Overview: Course structure and organisation. What is structural mechanics?
T2 Structural forms: Structural elements and examples. Strength and stiffness. Loads and factors
T3 Global Equilibrium: Forces and moments, point and distributed loads. Support conditions. Global equilibrium of structures. Concept of structural determinacy and indeterminacy
T4 Free Body Diagrams and Stress Resultant
Truss equilibrium. Stress resultants in struts (axial load), shafts (torsion), beams (shear and bending) and pressure vessels (membrane forces)
T5 Members carrying Axial Load
Simple mechanical behaviour. Deformation (due to load and thermal strain)
T6 Members carrying Torsion
Torsion of circular shafts and other closed sections. Torsional stiffness and deformation
T7 Stress Resultants in Determinate Beams (1)
Sign conventions. Shear force and bending moment diagrams
T8 Stress Resultants in Determinate Beams (2)
Relationships between w, V, and
T9 Bending of Beams (1)
Euler Beam Theory. Curvature. Plane sections. Bending strain
T10 Bending of Beams (2)
Euler Beam Theory. Elastic bending stresses. The neutral axis. Moment - curvature - stress - strain relationships
T11 Deflection of Beams
Double integration of curvature to find deflection. Support boundary conditions. Beam stiffness
T12 Superposition of Deflection
Deflection coefficients. Superposition of deflections
T13 Geometric Section Properties
Area, 2nd moments of area, Parallel axis theorem. Rectangular, circular, T and I section
T14 Composite Beam Sections
Modular ratio and equivalent section. Stress and strain diagrams
T15 Shear Stresses in Beams (1)
Complimentary shear. Derivation of shear stress formulae
T16 Shear Stresses in Beams (2)
Shear flow. Rectangular, box and flanged sections
T17 Combined Loading
Combining axial, torsion, shear and biaxial bending stresses
T18 Stress and Strain Transformation
Plane stress, plane strain. Mohr’s circle
Tutorials: - 9 ‘Tutorials’ (Format to be decided)
Come in with whatever things you had the most trouble with.
Laboratory experiments:
- 4-6 ‘Physical Experiments/Demonstrations’ (Format to be decided)
The truss lab is completed online.
All labs are completed before the relevant theory is taught. The point is foremost data collection.
Think about sources of error.
The report should wind up about 6 pages long (1.5 pages per experiment).
1.4 Total Hours: 100
- Lecture Hours 18,
- Seminar/Tutorial Hours 9,
- Supervised Practical/Workshop/Studio Hours 3,
- Online Activities 0.5,
- Summative Assessment Hours 1.5,
- Programme Level Learning and Teaching Hours 2,
- Directed Learning and Independent Learning Hours 66
1.5 Assessment
- Written exam 80 %
- Coursework 20 %
- Practical Exam 0 %
Note that the coursework is all one submission, which is intended to have been completed over the course of the course.
1.6 Learning Outcome
- Describe and manipulate fundamental concepts of stress, strain, and deformation in members carrying axial, bending, shear, and torsional loads;
- Determine how statically determinate trusses and beams carry load; for beams using diagrams of bending moment and shear force, and evaluate the resulting elastic deflections of the beams;
- Analyse structural cross sections, so as to determine the elastic stress and strain distributions, as well as the deformations, resulting from axial, bending and torsional actions;
- Describe and manipulate relevant concepts of combined loadings and stress and strain transformation.