Linear Differential Equations
Linear constant coefficient homogeneous differential equations
1 Introduction to Differential Equations
There are two main types of differential equations: Ordinary and partial. Partial differential lequations involve partial derivatives of vectors; ordinary differential equations do not. These are simpler to solve than partial DEs.
In \frac{df}{dx}, f is the dependent variable and x is the independent variable.
The order of a differential equation is the degree of the highest derivative occuring in that equation.
1.1 Linear vs Nonlinear
Linear equations are those equations in which the dependent variables and their derivatives do not occur as products, raised to powers or in nonlinear functions. Nonlinear equations are all other equations.
1.2 Homogeneous and Nonhomogeneous
1.2.1 How to arrange differential equations
The terms with the dependent variable go on the left hand side (ie x in \frac{dx}{dt}), and all terms not containing the dependent variable (either terms containing only the independent variable, in this case t, or constant terms) go on the right hand side of the equation.
1.2.2 Determining
When the terms are arranged properly, then if the right hand side of the equation is ZERO then the equation is homogeneous. If the right hand side (terms without the dependent variable) is NONZERO, then the equation is nonhomogeneous.
In other words, each term in a homogeneous differential equation involves a dependent variable or its derivatives.
2 Solutions to differential equations
The solutions to differential equations generally comprise a function space, or family of related functions.
2.1 1st order linear differential equations
For the equation a\frac{dx}{dt} + bx = 0, x \ne 0,
with constant coefficients a and b, the general solution is
x = Ae^{mt}, \textnormal{where } am + b = 0
2.2 Second Order DEs
Now consider what happens with a 2nd order DE:
a\frac{d^2x}{dt^2} + b\frac{dx}{dt} + cx = 0, a \ne 0
Substituting x(t) = e^{mt}, you get
\begin{gather} am^2e^{mt} + bme^{mt} + ce^{mt} = 0 \\ e^{mt}\left( am^2 + bm + c \right) = 0 \end{gather}
So x(t) = e^{mt} is a solution if am^2 + bm + c = 0.
am^2 + bm + c = 0 is the characteristic equation. It’s a quadratic; it has 2 roots m_1 and m_2.
2.2.1 Distinct real roots
When m_1 and m_2 are distinct real roots, then
x(t) = Ae^{m_1t} + Be^{m_2t} (all linear combinations of e^{m_1t} and e^{m_2t}.)
2.2.2 Complex roots
When m_1 and m_2 are complex conjugates, it’s slightly more complex. m_1 = \phi + j\psi and m_2 = \phi - j\psi.
Here’s a quick proof that complex roots must come as conjugates z = \phi + j\psi and z^\star = \phi - j\psi:
First suppose we have some polynomial P(x) = a_nx^n + a_{n-1}x^{n-1}+...+a_1x^1+a_0 such that P(\phi + j\psi) = 0. The binomial expansion of (\phi + j\psi)^n is
\psi^n + {n \choose 1}j\psi^{n-1}\phi + {n \choose 2}j^2\psi^{n-2}\phi^2 + ... + {n \choose n-1}j^{n-1}\psi\phi^{n-1} + j^n\phi^n.
Only the odd terms of this binomial expansion are imaginary; the even terms are real.
The binomial expansion of (\phi - j\psi)^n is
\psi^n + {n \choose 1}(-j)\psi^{n-1}\phi + {n \choose 2}(-j)^2\psi^{n-2}\phi^2 + ... + {n \choose n-1}(-j)^{n-1}\psi\phi^{n-1} + (-j) ^n\phi^n.
Comparing the two binomial expansions, the odd terms have switched sign. This means that the imaginary part of the second binomial expansion is the exact negative of the imaginary part of the first binomial expansion; powers of complex conjugates remain conjugates.
Since exponentiation and multiplication by a constant preserve conjugacy, P(z^\star) = P(z)^\star. Since P(z) = 0, and 0^\star = 0, P(z^\star) = 0 for all P(z) = 0.
\begin{align} x(t) &= Ae^{\phi + j\psi t} + Be^{\phi - j\psi t} \\ &= e^{\phi t} \left( Ae^{j\psi t} + Be^{-j\psi t}\right) \\ &= e^{\phi t}[(A + B)\cos{\psi t} + j(A - B)\cos{\psi t}] \end{align}
You may further simplify by making A + B = C and A - B = D.
2.2.3 The Same Root
If m_1 = m_2 = k, then the general solution with linear superposition breaks down (the function vectors are no longer linearly independent and are not sufficient to span a function space).
For a differential equation to have a repeated root at m = k, then the characteristic quadratic must be a square:
\begin{gather} am^2 - 2akm + ak^2 = 0 \\ a(m - k)^2 = 0 \end{gather}
Then the differential equation takes this form:
a \frac{d^2x}{dt^2} -2ak \frac{dx}{dt} + ak^2x = 0
Take the “test solution” x(t) = t^p e^{mt}. Then \frac{dx}{dt} = p\left(t^{p-1} \right)e^{mt} + m t^p e^{mt} by the power rule and product rule, and \frac{d^2x}{dt^2} = m^2 t^p e^{mt} + 2 \left( m p t^{p-1} e^{mt} \right) + p(p-1)t^{p-2}e^mt.
Substitute these expressions into the differential equation:
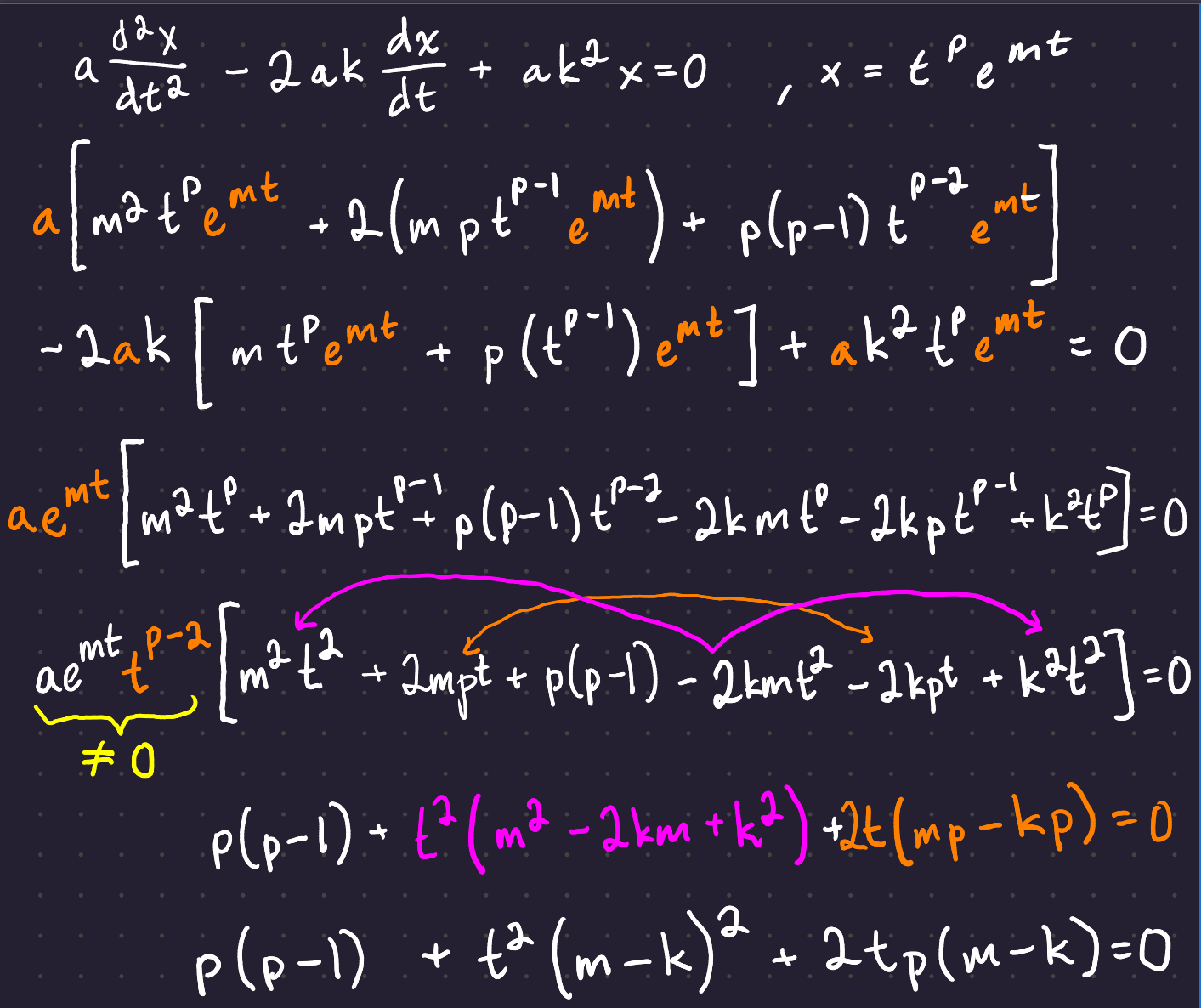
For the result to hold, it must be the case that m = k and p \in \{ 0,1 \}. Going back to our test solution, we see that either x(t) = e^{mt} or x(t) = te^{mt}. Taking the space spanned by these two functions, we find that
\begin{gather} x(t) \in \texttt{span}\left(e^{mt}, te^{mt}\right) \\ x(t) = Ae^{mt} + Bte^{mt} \\ x(t) = (A + Bt)e^{mt} \end{gather}
3 Conclusion
To solve a linear homogeneous constant coefficient differential equation, find the roots of the characteristic equation with all nth order derivatives replaced with nth powers of x. Then the solutions are the space spanned by all e^{\textnormal{(root)}t}, multiplied by a power of t every time a root repeats.