Materials
The selection of a material for a machine part or a structural member is one of the decisions the designer is called upon to make. After choosing the material and process, the designer can then proportion the member so that the internal stresses andstrains have reasonable and satisfactory values compared with the properties associated with failure of the material.
1 Static Strength
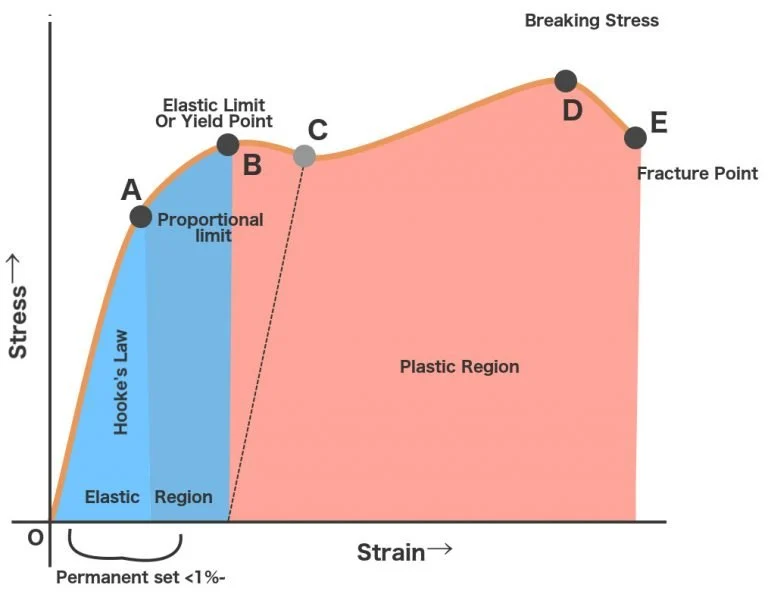
A sample of material with a simple cross section is placed in a loading machine and stressed. The following graph shows the relationship between stress, \sigma (applied force divided by cross-sectional area) and strain, \epsilon (proportional change in length).
 {#fig-stress, width=60%}
{#fig-stress, width=60%}
Point A on the graph is the proportional limit, which is the point at which th ecurve first deviates from a straight line. Below that point, stress and strain are perfectly proportional; Hooke’s Law applies in this region. Many materials reach a point at which strain increases rapidly (the material starts stretching) without a corresponding increase in stress. This is the yield point. Before the elastic limit (B in the diagram), no permanent set will be observed. The sample returns to its original length when removed from the machine. If the material is pulled beyond the elastic limit, a permanent set will occur. The yield point, beyond which the material loses its strength, is determined as the stress needed to create a certain % increase in permanent set, usually 0.2 or 0.5% of the original gauge length. That point is point C in the diagram. Further on, point D represents the ultimate or tensile strength, the maximum stress reached within the part. E is the fracture point. Some materials fracture when the stress-strain locus is still rising (cast irons, HSS) and some materials fracture after a short period of decreasing internal stress.
Be careful to distinguish strength and stress. Strength is an intrinsic and unchangeable property of a part; stress is a transient property. Stresses often occur when a part is loaded in a machine, but they could preexist in a part (as with tempered glass). The strength of a part will be determined before you use it, but the stress within a part is determined by you.
The same process as is used for a tensile stress-strain test may be used for a compressive test or even a torque test. In the case of torque, the results are plotted on a torque-twist diagram.
All of the strengths calculated through these diagrams are referred to as engineering strengths or nominal strengths because they are calculated using the original cross-sectional area of the part. This makes them more useful, since the cross-section of an unstressed part is what you get on McMaster. But it means they don’t quite correspond with the reality of the part when tensioned. This is mildly important and highlights the big difference between engineers and physicists - we are mainly interested in quantifying behavior insofar as it aids in the design process.
1.1 True stress-strain Diagrams
2 Strength and Cold Working
Cold working is the process of stressing or deforming a material in the plastic region of the stress-strain diagram without applying heat.