AC Power Systems Part 1
Power dissipation of a load in an AC power system
When you connect a load across a current source, the power consumed is the product of the voltage across the load and the current flowing through that load.
In a DC current, this relationship takes the simple form
P = VI, \tag{1}
since the voltage across the load and the current flowing through it are constant with respect to time.
When voltages and currents are sinusoidal, however, as in an ac circuit, the situation is more complex. There might be a phase difference between V and I. The instantaneous power is still the same as in Equation 1, but the average power supplied to the load will be affected by the phase angle between the voltage and the current.
\begin{align} p &= vi \\ &= V_m\sin (\omega t + \phi_V) \, I_m \sin (\omega t + \phi_I) \\ &= V_m\,I_m \frac{1}{2}(\cos (\omega t + \phi_V - \omega t - \phi_I) - \cos (\omega t + \phi_V + \omega t + \phi_I)) \\ &= \frac{V_m I_m}{2} \cos(\phi_V - \phi_I) - \frac{V_m I_m }{2}\cos(2\omega t + \phi_V + \phi_I) \end{align}
The final expression for power has a constant portion \frac{V_m I_m}{2} \cos(\phi_V - \phi_I) and a term which alternates with time. The magnitude of the constant component is ddetermined both by the magnitude of the current and voltage and by the phase relationship between the voltage and current. This constant component is the average power dissipated by the load.
The power has an AC component \frac{V_m I_m }{2}\cos(2\omega t + \phi_V + \phi_I), whose magnitude is determined by the magnitude of the voltage and the current, and whose frequency is twice the line frequency.
Since the instantaneous value of power is oscillating with twice the line frequency, the work we can do oscillates.
1 Different Offsets
If you have a resistor across a voltage source, the current is directly in phase with the current, and so the constant portion of power goes to \frac{V_m I_m}{2} \cos(\phi_V - \phi_I = \frac{V_m I_m}{2}.
The power in this case is never negative:
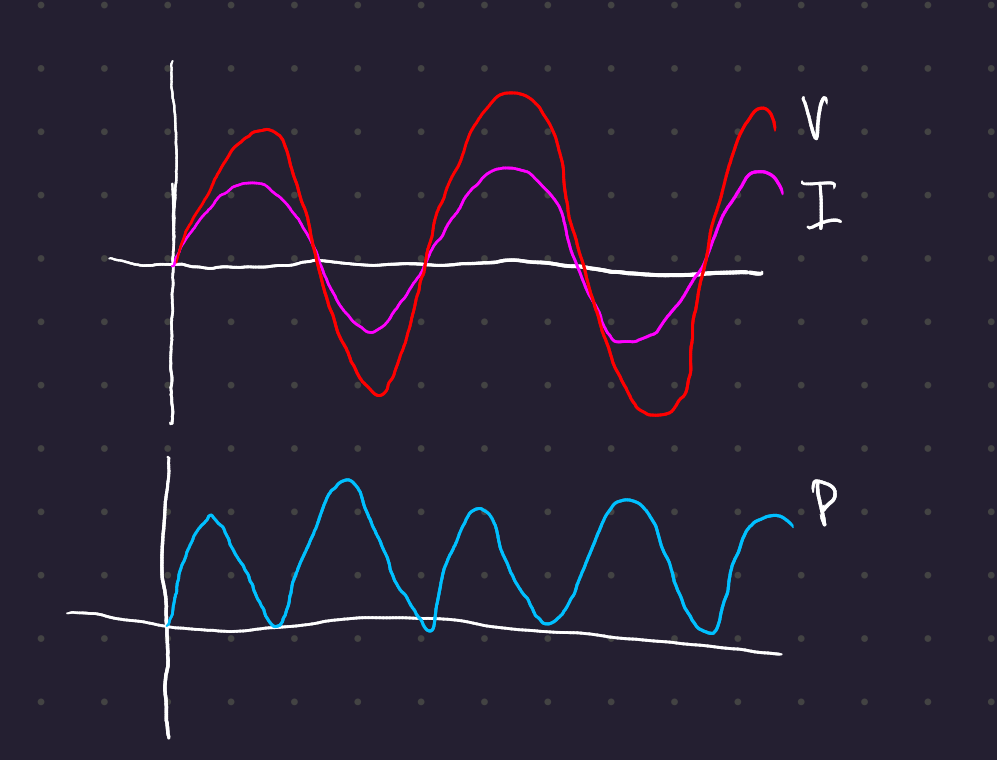
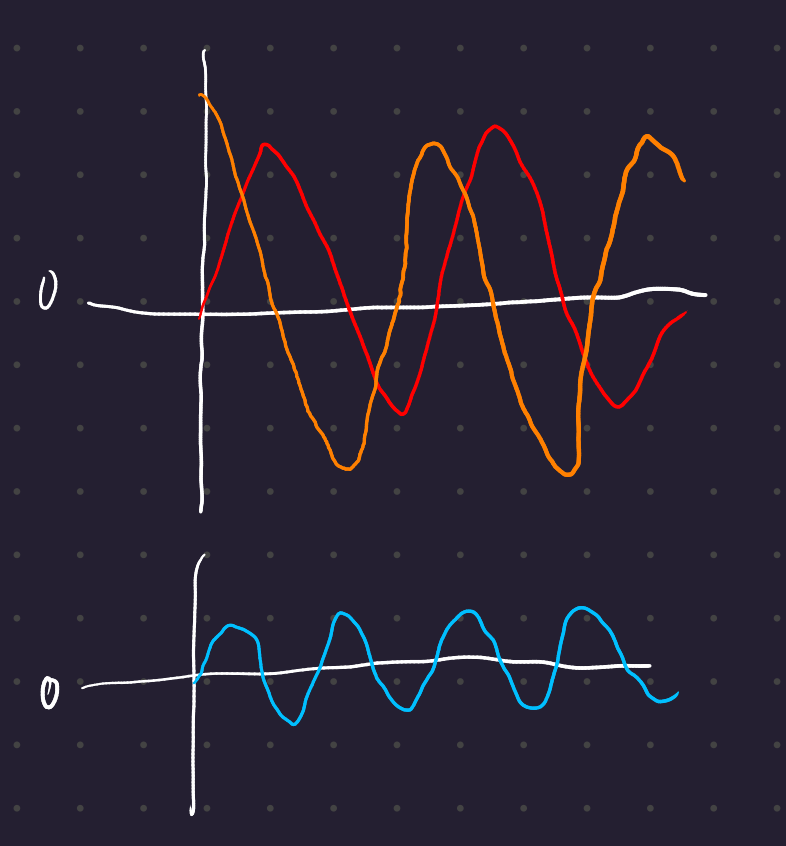
If the voltage and current are offset from each other by 90° (as might happen in an inductive or capacitive load), then no power is dissipated even though current is flowing: the constant term goes to 0.
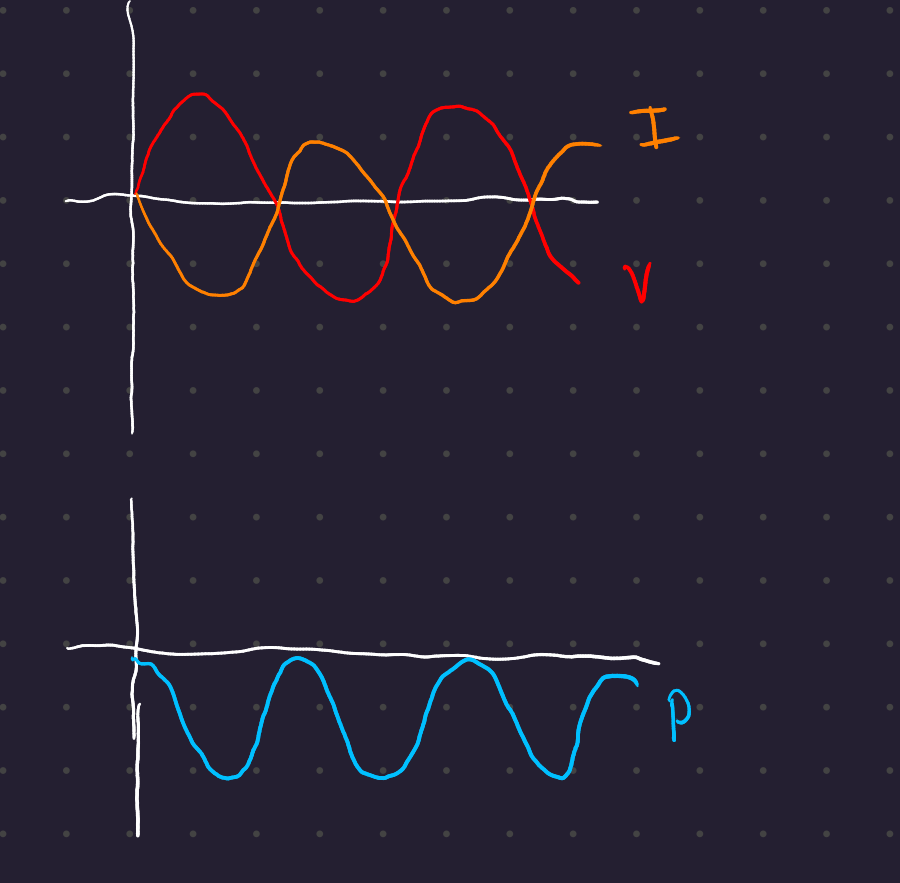
And in the final case, when current and voltage are offset by 180° away from each other, the power is consistently negative. This is the case in any power generating station, solar PV, or battery bank supplying energy to the grid.
Make sure to keep in mind that the values for V_m and I_m are peak voltages and currents!