Inhomogeneous Linear Differential Equations
Lecture 3
Definition 1 (Inhomogeneous) Consisting of terms that are not all of the same degree or dimensions.
1 The Particular Integral
The general form of an inhomogeneous linear constant coefficient DE is:
\begin{align} L[x] &= a_{p} \frac{d^px}{dt^p} + a_{p-1} \frac{d^{p-1}x}{dt^{p-1}} + a_{p-2} \frac{d^{p-2}x}{dt^{p-2}} + ... \\ &+ a_{2} \frac{d^{2}x}{dt^{2}} + a_{1} \frac{d^{1}x}{dt^{1}} + a_{0} \frac{d^{0}x}{dt^{0}} = f(t) \end{align} \tag{1}
where L[x] is a p-th order differential operator.
Theorem 1 Let
L[x] = f(t) \tag{2}
be aninhomogeneous linear differential equation. If x^* is any solution of Equation 2, and x_c is a solution of the equivalent homogeneous differential equation
L[x] = 0,
then x^* + x_c is also a solution of Equation 2.
The proof of Theorem 1 is very straightforward.
Proof. We know that L[x^*] = f(t) and L[x_c] = 0. Since L[x] is a linear operator, you may expand L[a + b] into L[a] + L[b]. Then
\begin{align} L[x^* + x_c] &= L[x^*] + L[x_c] \\ &= f(t) + 0 \\ &= f(t) \end{align}
So x^* + x_c is a solution of Equation 2.
x^* is the particular integral, and x_c is the complementary function.
This is very parallel to linear algebra. We started by finding the nullspace of the linear operatox L, ie the space of functions for which L[x] = 0. Now we find the general transformation L[x] = f(t), similar to A\textbf{x} = \textbf{b}.
Recall the Big Picture
A\left(\textbf{x}_{row} + \textbf{x}_{null}\right) = \textbf{b}_{column}
with this accompanying picture:
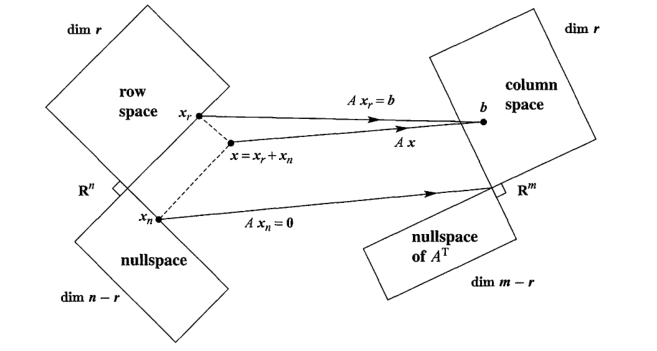
Every vector in the row space of A corresponds to a particular vector in the column space of A, and the set of solutions to A\textbf{x} = \textbf{b} is that vector plus the nullspace of A. Vectors in the left nullspace of A have no solution to A\textbf{x} = \textbf{b}.
Similarly, there is a family of functions in the nullspace of L, the family of solutions to the homogeneous differential equation L[x] = 0. Each function f(t) on the right hand side corresponds to a particular function in the row space of L, which we call the particular integral x^*. Then the full solution set to L[x] = f(t) is that function plus the nullspace of L.
So the question is, how do you find a particular integral? - empirical rules - inspiration - trial and error - give up
2 Solving a Polynomial RHS
Find the general solution of
\frac{d^2x}{dt^2} + 5 \frac{dx}{dt} - 6x = t^2. \tag{3}
To find the space of complementary functions x_c, take the characteristic equation
m^2 + 5*m -6 = 0
with roots m \in \{ 1, -6 \}.
The nullspace of L[x] is then x(t) = Ae^{t} + Be^{-6t}. \tag{4}
2.1 Finding the particular integral
To find a particular integral, test with the polynomial
x(t) = Pt^2 + Qt + R.
This function is our trial integral, which is a “completely arbitrary” choice.
Substituting x(t) into Equation 3 gives
\begin{gather} 2P + 5\left( 2Pt + Q \right) - 6(Pt^2 + Qt + R) = t^2 \\ (-6P)t^2 + (10P -6Q)t + (2P + 5Q -6R) = t^2 \\ \end{gather} {eq-polynomial}
Solving ?@eq-polynomial is fairly straightforward: each of the coefficient terms must equal zero, so we set up a system of linear equations and back-substitute our solutions.
\begin{cases} -6P &&&=1 \\ 10P &-6Q & &= 0 \\ 2P &+ 5Q &-6R &= 0 \\ \end{cases}
Solving through back-substitution, P = -\frac{1}{6}, Q = -\frac{5}{18}, R = -\frac{31}{108}.
Then the particular integral is -\frac{1}{6}t^2 -\frac{5}{18}t -\frac{31}{108}.
2.2 The general solution
To find the general solution, we add back in the nullspace of L[x], which we defined in Equation 4:
-\frac{1}{6}t^2 -\frac{5}{18}t -\frac{31}{108} + Ae^{t} + Be^{-6t}.
You can do this with any polynomial RHS - just use the fully general polynomial of the same degree as your test case.